Solids are rigid and possess definite shape and volume. In solids, ions atoms or molecules are held together by strong inter ionic, interatomic, or intermolecular forces. The properties of the solids depend upon the nature of constitutional particles and the binding forces operating between them.
This chapter is very important for CBSE and ISC exams. Here I will try to make the chapter easy for you by focusing on the main points. Don’t forget to complete the Short Question and Answer, MCQ Test and Practice Set of this Chapter. Link at the end of this post.
Types of solids:
We normally get two types of solids-Crystalline and amorphous. The difference between them are-
| Characteristics | Crystalline solids | Amorphous solids |
| Nature of arrangement of constituent particles in space | Definite and regular | Irregular |
| Nature of solids | True | Pseudo |
| Order of arrangement of the particles | Long | Short |
| Nature of physical properties | Anisotropic | Isotropic |
| Melting point | Sharp | Over a certain range of temperature |
| Enthalpy of fusion | Define | Not definite |
| Cleavage | Can be cleaved along definite planes | On cleavage gives irregular fractures |
Classification of solids based upon the nature of inter-particle forces:
Depending upon the nature of binding force, solids are classified as ionic, covalent, molecular and metallic solids.
The comparative of the solids are-
| Characteristics | Ionic solids | Covalent solids | Molecular solids | Metallic solids |
| Constituent particles | Cation and anion | Atoms | Molecules | Kernels(+ve charge) and mobile electrons |
| Binding force | Strong coulombic electrostatic force | Covalent bonding | London forces, dipole-dipole interaction, hydrogen bonding | Metallic bonding |
| Electrical conductivity | Insulators in solid state but conducting in molten state | Insulator | Insulator | Insulators in solid state as well as in molten state |
True solid
A true solid may be defined as a matter which possesses rigidity, definite shape, definite volume, and long-range of order.
Pseudo solid
Pseudo solids have a shape but can be easily distorted. Ex-Glass, pitch.
Isotropic substances and anisotropic substances
- The substances which have the same physical properties such as electrical conductivities, refractive index, thermal expansion, mechanical strength, etc. identical in all directions in the space are called isotropic substances. This property is known as isotropy. Amorphous substances are isotropic.

- The substances which have different physical properties in all directions in the space are called anisotropic substances and the property is called anisotropy. Crystalline solids are anisotropic.

Unit cell
Unit cell is the smallest three-dimensional groups of lattice points, which when repeated in three dimensional in space, give the whole lattice of the crystal.
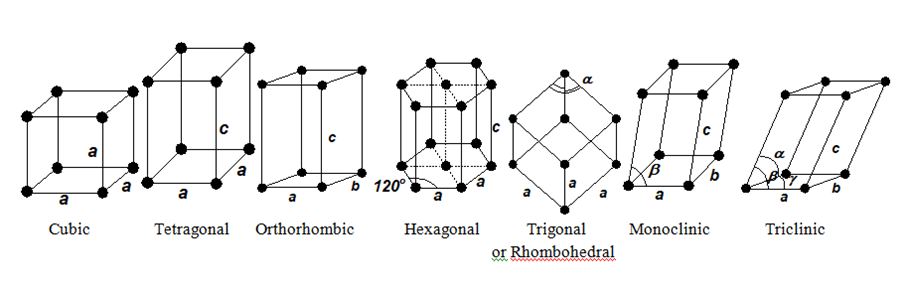
Seven Crystal system
- To describe a unit cell, six parameters are required. (a, b and c are the three sides and α,β, and γ are the three angles

- Based upon certain rotation axes, crystals are classified into seven categories called seven Crystal System.
- Based on these seven crystal systems and the four possible variations, there are 14 possible three-dimensional lattices. These are called Bravais lattices.
- Among the seven crystal systems, cubic is the most symmetric whereas triclinic is the most unsymmetrical system.
| Unit Cell | Axial distance | Axial angles | Example |
| Cubic | a=b=c≠ | α=β=γ= 900 | NaCl, Diamond, KCl, ZnS, Cu, Ag, Alum, CaF2 |
| Tetragonal | a =b ≠ c | α=β=γ= 900 | TiO2, SnO2, CaSO4, Sn(White), ZrSiO4 |
| Orthorhombic | a≠b≠c | α=β=γ= 900 | Rhombic S, BaSO4, KNO3, K2SO4, PbCO3 |
| Hexagonal | a b≠c | α=β= 900 γ= 1200 | Graphite, CdS, PbI2, Mg, ZnO |
| Trigonal or Rhombohedral | a=b=c | α=β=γ≠900 | CaCO3( Calcite), HgS, quartz, NaNO3 |
| Monoclinic | a≠b≠c | α=γ= 900≠β | Monoclinic S, PbCrO4, Na2SO4,10H2O |
| Triclinic | a≠b≠c | α≠β≠γ≠900 | K2Cr2O7, CuSO4.5H2O, H3BO3 |
Space lattice and crystal lattice
Space lattice is the regular pattern of points, which describes the three dimensional arrangement of particles in a crystal structure. When the points are replaced with actual atoms or ions, it is called crystal lattice.
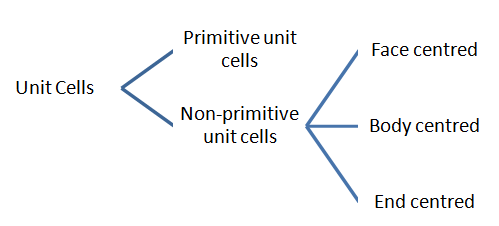
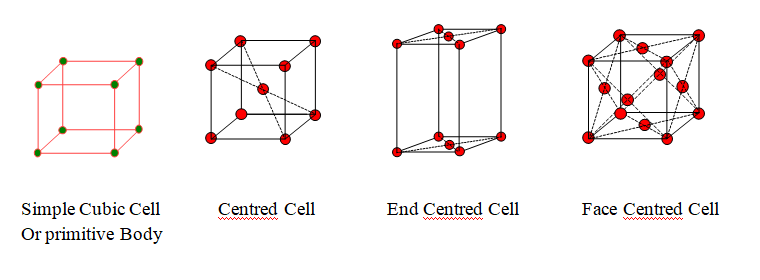
Types of unit cells
Rank or No of Particles in a Unit Cell
| Unit Cell | Position of constituent particles | No of atoms at corners | No of atoms at faces | No of atoms at centre | Total |
| Simple Cubic Cell or primitive | At the corners only | 1 | 0 | 0 | 1 |
| Body Centred Cell | At the corners as well as in the centre | 1 | 0 | 1 | 2 |
| End Centred Cell | At the corners as well as at the centre of any two opposite faces | 1 | 1 | 0 | 2 |
| Face Centred Cell | At the corners as well as in the centre of each face | 1 | 3 | 0 | 4 |
Close packing
Constituent particles of a crystal pack in such a way that the volume is minimum and density become maximum and attain stability. This type of packing is called close packing.
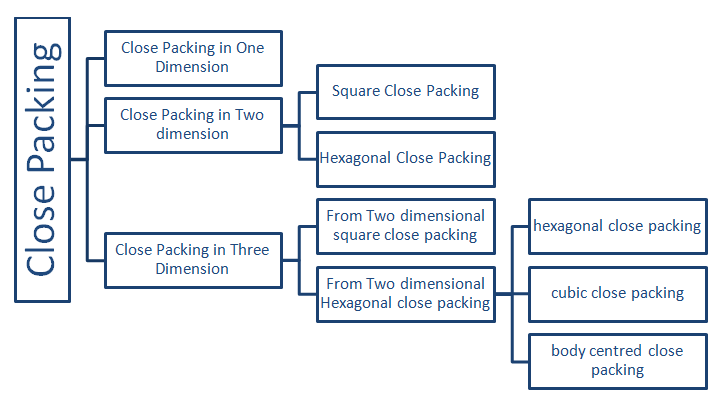
1. Close Packing in One dimension

Each sphere touch one another making a line arrangement. C.N= 2
2. Square Close Packing in Two Dimensions
Each sphere remains attached with 4 other spheres. C.N=4
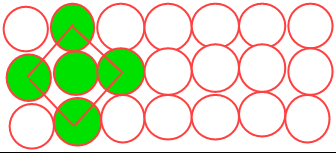
3.Hexagonal Close Packing in Two Dimensions

The spheres in the second row are placed in the gaps between the spheres of the first row. Each sphere touches 6 neighboring spheres. C.N=6
4. Three dimensional close packing from two dimensional square close packed structures
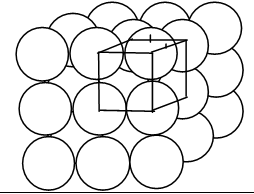
The second layer is placed over the first layer such that the spheres of the upper layer are exactly above those of the first layer.
5. Three dimensional packing (hcp)
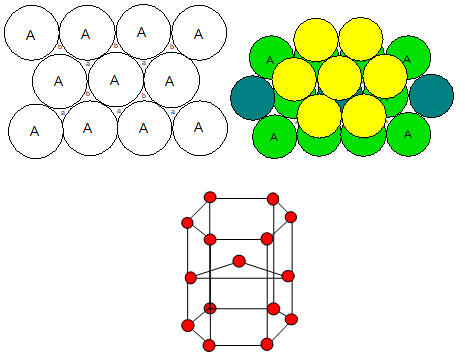
The third layer may be placed above the second layer such that the tetrahedral voids of the second layer are covered by the spheres of the third layer. The spheres of the third layer are exactly aligned with those of the first layer.
This structure is called a hexagonal close-packed (hcp) structure. Ex: Mg, Be, Zn, Cd, Ti, Zr
6.Three dimensional packing (ccp)
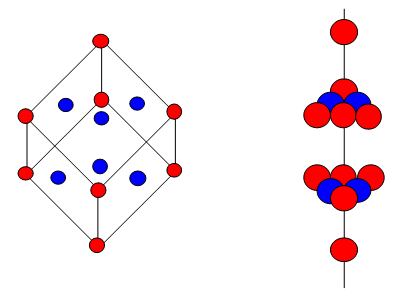
The third layer may be placed above the second layer such that the octahedral voids of the second layer are covered by the spheres of the third layer. The spheres of the third layer are not aligned with those of the first or second layer.
This structure is called cubic close packed (ccp) or face centred cubic (fcc) structure.
Ex: Fe, Cu, Ag, Au, Al, Pt, Co
Crystal structure of common metals
| Structure | Metals |
| Hcp | Na, Mg, Be |
| Ccp or fcc | Fe,Ni,Cu,Ag,Au,Al |
| Bcc | Li,Na,K,Pb,Ba,Cr,Fe,Mn |
| Simple cubic | Po |
All noble gases have ccp structure, except He which has hcp structure.
Voids
- The space which is left in between the particles of a closest packed arrangement.
- Trigonal voids: voids present in triangular spaces in 2-dimentional packing .
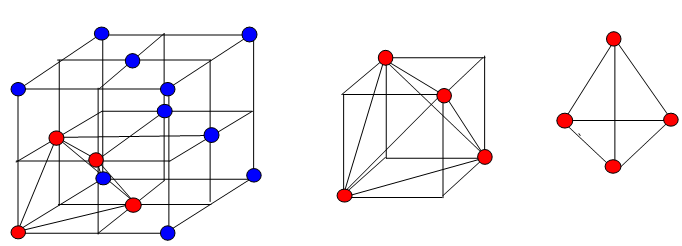
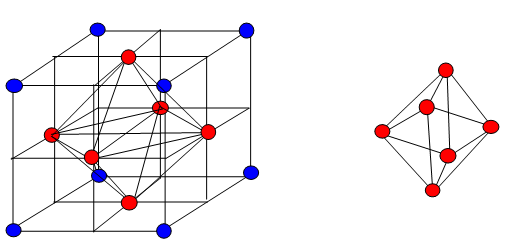
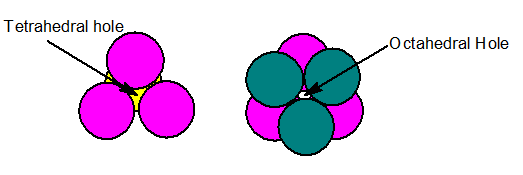
- In 3-dimention we get tetrahedral and octahedral voids.
| Tetrahedral voids | Octahedral voids |
| Radius of tetrahedral voids=22.5% of the sphere | Radius of octahedral voids=41.4% of the sphere |
| C.N=4 | C.N=6 |
| Radius of tetrahedral voids= 0.225R | Radius of octahedral voids = 0.414R |
| There are two tetrahedral voids per sphere | There is one octahedral void per sphere |
Number of voids filled and formula of the compound
- The number of octahedral voids = number of particles present in the close packing.
- The number of tetrahedral voids= 2 x Number of octahedral voids.
- Usually, in ionic compounds, anions are present in the packing whereas cations occupy the voids.
Coordination number: It is the number of equidistant neighbour atoms that an atom has in its crystal structure.
The relation between a, r and d of the unit cell
a= Edge length, r= radius of atom, d= nearest neighbour distance or inter ionic distance.
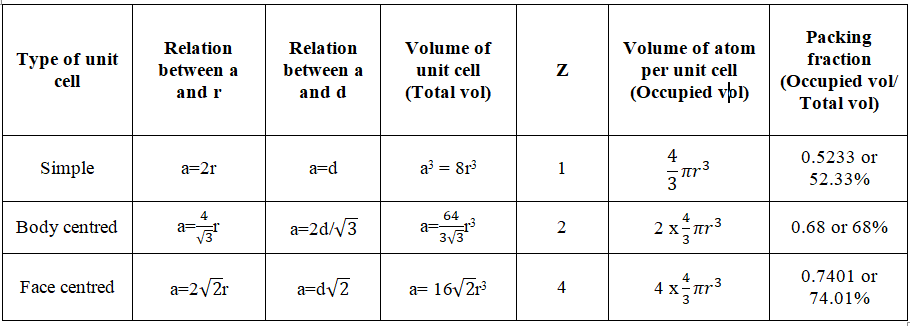
Radius Ratio
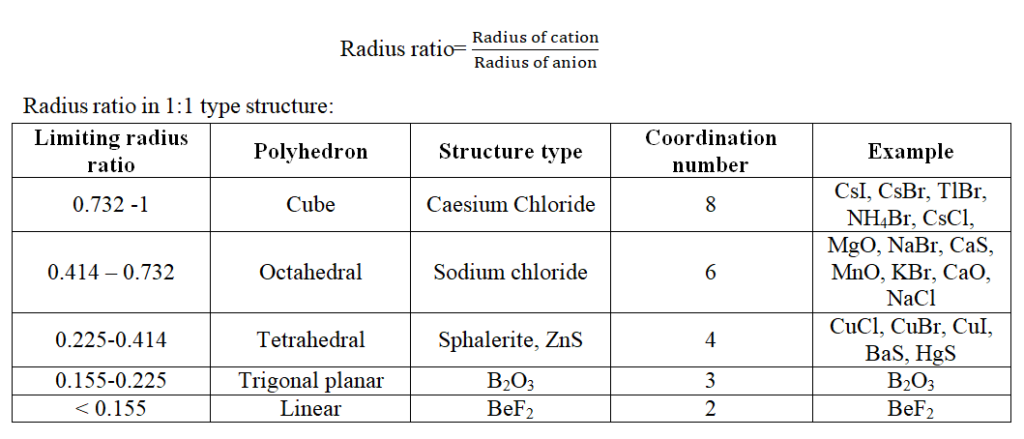
Packing Fraction
Packing Fraction is equal to the ratio of the volume occupied by the atoms present in a unit cell to the total volume of the unit cell.
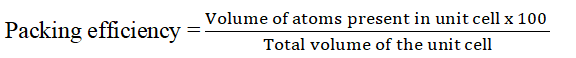
Packing fraction shows how closely the atoms are packed together in a unit cell. The packing density decreases in the order: fcc> bcc> Simple cube.
Derivation of packing efficiency
Simple cubic unit cell:
- Let ‘a’ be the edge length of the unit cell and r be the radius of the sphere.
As sphere are touching each other
Therefore a = 2r
No. of spheres per unit cell = 1/8 × 8 = 1
Volume of the sphere = 4/3 πr3
Volume of the cube = a3= (2r)3= 8r3
∴Fraction of the space occupied =1/3πr3/ 8r3= 0.524
∴% occupied = 52.4 %
Body-centred cubic unit cell:
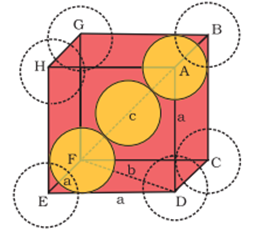
In Triangle EFD
Let DF= b and we know that ED=EF= a (edge length)
Now, b2= a2+ a2= 2a2
In Triangle AFD
Let, AF = c and we know that FD = b & AD = a (edge length)
Now, c2= a2+ b2=a2+ 2a2= 2a2
or c =√3 a
We know that c is body diagonal.As the sphere at the centre touches the sphere at the corner. Therefore body diagonalc = 4r
i.e.√3 a = 4r
or r = (√3/4)a
or a = 4r /√3
∴Volume of the unit cell = a3= (4r / √3)3= 64r3/ 3√3
No. of spheres in bcc = 2
∴The volume of 2 spheres = 2×4/3πr3
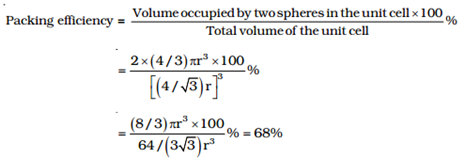
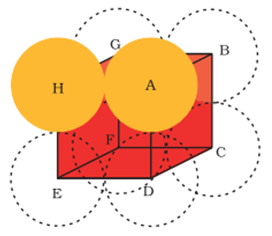
Face-Centred Cubic (hcp and ccp Structures)
Let ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube
As there are 4 sphere in fcc unit cell
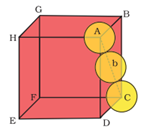
∴The volume of four spheres = 4 (4/3πr3)
In fcc, the corner spheres are in touch with the face centred sphere. Therefore, face diagonal AD is equal to four times the radius of sphere AC= 4r,
But from the right angled triangle ACD , AC = √AD2+ DC2=√a2+a2=√2a
4r = √2a or a = 4/√2 r
∴volume of cube = (2/√2 r)3
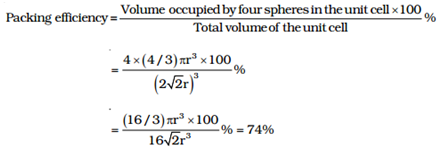
Calculation of density of a crystal
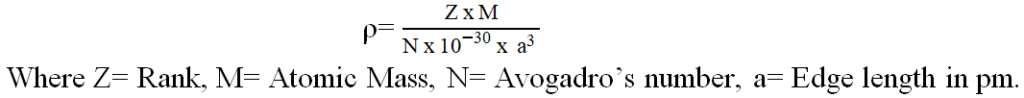
Defect
Any irregularities of constituent particles from perfectly ordered arrangement in a crystal is called defect.
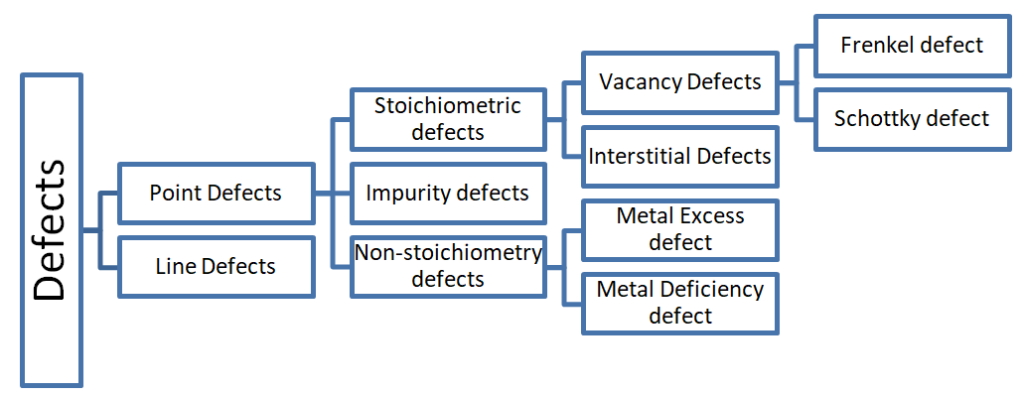
1.Point Defect
Irregularities from ideal arrangement around a point or an atom in a crystalline substance.
2.Line Defect
Irregularities from ideal arrangement in entire rows of lattice points.
3. Stoichiometric Defect
These are the point defects that do not disturb the stoichiometry of the solid. The ratio of the cations and anions remains same.
4. Vacancy Defect
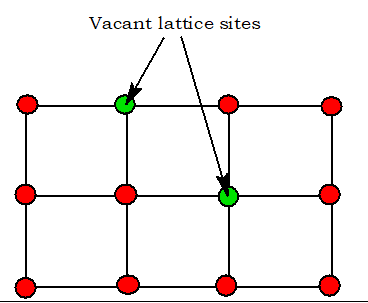
When some of the lattice sites are vacant, the crystal is said to have a vacancy defect. Density decreases. Seen in non-ionic solids.
5. Interstitial defect

When some constituent particles also occupy an interstitial site, the crystal is said to have interstitial defects. Density increases. Seen in non-ionic solids.
6. Frenkel defect
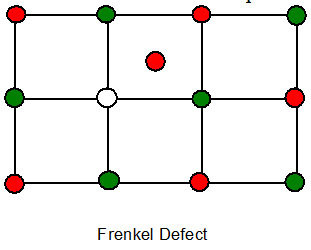
Cation is dislocated from its normal site to an interstitial site.It creates a vacancy defect at its original site and an interstitial defect at its new location.
Seen in ionic substances which have low coordination no and in which there is a large difference in the size of cation and anion.
Ex: ZnS, AgCl, AgBr, AgI.
The ionic compound remains electrically neutral and stoichiometrically same.This defect increases the temperature.
7. Schottky defect
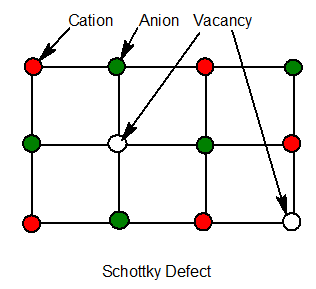
In an ionic compound if equal no of cations and anions are missing, it is called schottky defect.
8. Impurity Defect
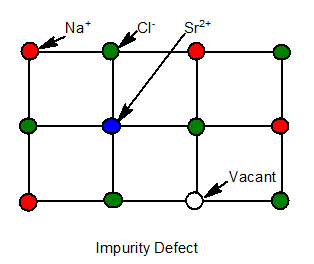
When some foreign particles are present in the crystal.Ex: Molten NaCl containing little amt of SnCl2 .
9. Metal excess defect due to anionic vacancies.
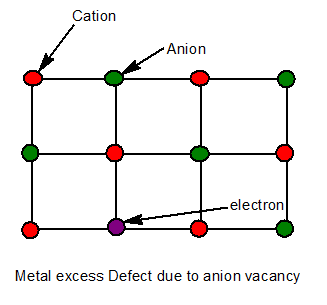
A negative ion is missing from its normal site in the lattice. Thus the metal ion becomes in excess. The hole caused by the absence of negative ion is occupied by an electron to maintain electrical neutrality.
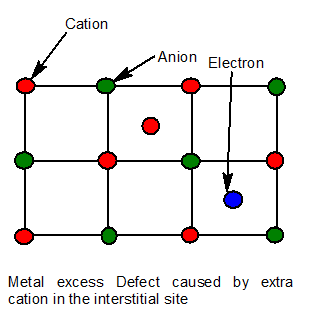
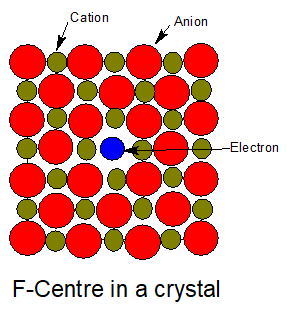
The electrons trapped in anion vacancies are referred to as F-Centre(F-Farbe which means colour)
10.Metal deficiency defect
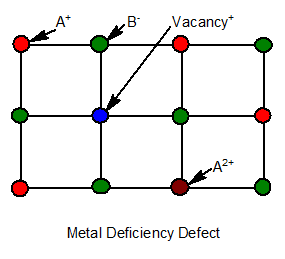
It is due to missing of a cation of a lower valence and another lattice site occupied by a cation of higher valence.
Ex: FeO, FeS, NiO etc. It is seen in those metals which show variable valencies.
Characteristics of crystalline solids
| Name | Type | Characteristics |
| NaCl | Ionic | 1. The radius ratio of Na+ and Cl- ion is 0.525 2. The chloride ions adopt a ccp or fcc arrangement. 3. Sodium ions occupy the octahedral voids. They are present at the edge center and the body center. 4. The C.N of Na+ and Cl- ion is six. 5. Number of Na+ and Cl- present per unit cell is 6. Thus the formula of sodium chloride is NaCl 7. An increase in pressure increases the coordination number of Na+ and Cl– ions and NaCl acquires CaCl structure. |
| Diamond | Atomic or Network or Covalent Solids | 1. Face centered cubic structure. 2. Each carbon is sp3 hybridized. The C-C bond length is 1.54Ǻ and bond angle is 109 degree 28 min. 3. Each carbon atom is bonded tetrahedrally to four other carbon atoms by covalent bonds. 4. The coordination number of each carbon atom is 4. |
| Graphite | Atomic or Network or Covalent Solids | 1. In graphite, each carbon possesses sp2 hybridization. 2. Each carbon is bonded with three neighboring carbon atoms lying in the same plane, to give rise hexagonal rings, and thus the coordination number of carbon is graphite is 3. 3. The hexagonal rings constitute a sheet-like structure. The sheets are held together by van der Waal’s forces. 4. The C-C bond length is 1.415Ǻ and the distance between the two sheets is 3.4 Ǻ. |
| Copper | Metallic | 1. Cu possesses a face-centered cubic. 2. In the lattice of copper, each Cu2+ ion is surrounded by twelve Cu2+ ions. Out of the twelve, six are present in one plane while the three above the plane and remaining three below the plane. 3. The coordination number of Cu is 12. 4. A similar type of structure is found in Ag, Au, Al, and Pb. |
Structure of simple ionic crystals
- AB type: It is of three types:
- Rock salt (NaCl) type.Halides of Li, Na , K and CsF, Halides of ammonium, Oxides and sulphides of Mg, Ca, Sr and Ba, AgCl, AgBr, CaCO3, CaC2.
- CsCl: CsBr, CsI, TlCl, TlBr.
- ZnS: Chloride , bromide and iodide of Cu, AgI, BeS.
- AB2 type: CaF2, BaF2, BaCl2, SrF2, SrCl2, CdCl2, PbF2.
- A2B type: Na2O, Li2O, K2O, Rb2O, Rb2S.
Effect of pressure and temperature on crystal structure
An increase in temperature decreases the coordination number whereas increase in pressure increases the same. At about 760 K, CsCl (C.N=8:8) changes to NaCl (C.N=6:6) structure. Applying pressure during crystallisation, NaCl changes to CsCl structure.
Nature of bonding in metallic solids is explained by
- Electron sea or electron gas theory
- Molecular orbital theory or Band theory
Band, valence band and conduction band
The atomic orbitals of the metal atoms are close in energy. They overlap to form molecular orbitals which are very close in energy to each other. This set of molecular orbitals is called a band. The band formed from atomic orbitals of lower energy is called valence band. It holds the valence electrons.Conduction band is formed from empty or partially filled atomic orbitals of higher energy.In conductors, the energy difference in the valence band and conduction band is negligible.
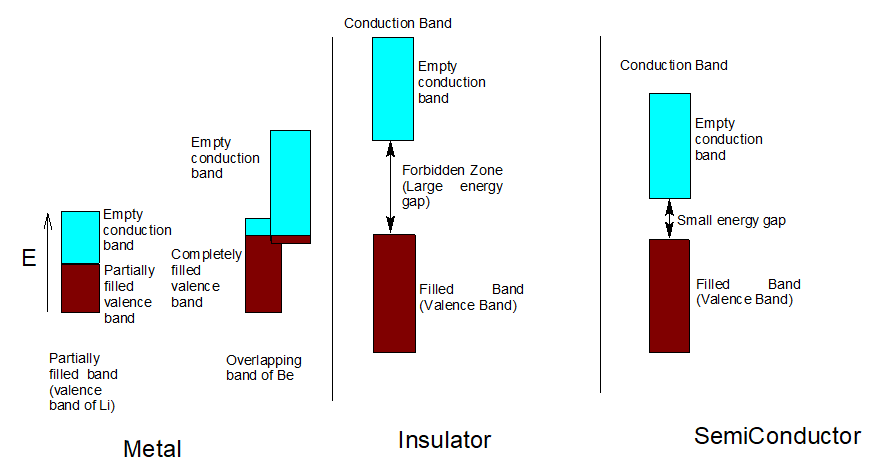
In semiconductors, there is a small energy gap and in insulators, there is a large energy gap. As electrons jump from valence band to conduction band, the conductivity of electricity takes place. As the gap between the bands’ increases, the conductivity decreases.
Types of semiconductors
- Intrinsic semiconductors: The substances which are insulator at room temperature and become semiconductor when heated or irradiated with light are intrinsic semiconductor.
- Extrinsic semiconductor: These are formed by adding impurity to the insulator (dopping).They are of two types:
- n-type semiconductor: The term n-type comes from the negative charge of the electron. In n-type semiconductors, electrons are the majority carriers and holes are the minority carriers. n-type semiconductors are created by doping an intrinsic semiconductor with donor impurities.
- p-type semiconductor: The term p-type refers to a positive charge of the hole. As opposed to n-type semiconductors, p-type semiconductors have a larger hole concentration than electron concentration. In p-type semiconductors, holes are the majority carriers and electrons are the minority carriers. p-type semiconductors are created by doping an intrinsic semiconductor with acceptor impurities.
| Intrinsic semiconductor | Donor atoms | Acceptor atoms | |
| Group IV semiconductors | Silicon, Germanium | Phosphorus, Arsenic, Antimony | Boron, Aluminium, Gallium |
| Group III-V semiconductors | Aluminum phosphide, Aluminum arsenide, Gallium arsenide, Gallium nitride | Selenium, Tellurium, Silicon, Germanium | Beryllium, Zinc, Cadmium, Silicon, Germanium |
Effect of temperature on the electrical conductivity of-
| Metals | Electrical conductivity decreases with the increase in temperature |
| Semiconductor | Electrical conductivity increases with the increase in temperature |
Magnetic property of metals
| Property | Caused By | Examples |
| Diamagnetism | Those materials which do not contain unpaired electrons. They are weakly repelled by magnetic field. They are weakly magnetized in a magnetic field in opposite direction. | NaCl, TiO2, Benzene, V2O5, Cu+ , Zn2+ N2, KCl etc. |
| Paramagnetism | Those materials which contain unpaired electrons. They are weakly repelled by magnetic field. It lose their magnetism in the absence of magnetic field. They lose their magnetism in the absence of magnetic field. They are magnetized in magnetic field in the same direction. | O2, Cu2+, Fe2+, Fe3+, Cr3+, TiO, Ti2O3, VO,VO2 etc. |
| Ferromagnetism | The solids which are strongly attracted by external magnetic field and show permanent magnetism even when the external field is removed. It is due to spontaneous alignment of magnetic moments in the same direction. | Fe, Co, Ni |
| Antiferromagnetism | They have equal number of parallel and antiparallel electrons. The net magnetic moment is zero even though unpaired electrons are present. | MnO, MnO2, MnO3, V2O3, FeO, Fe2O3, NiO |
| Ferrimagnetism | The solids with very small net magnetic moments, inspite of having large number of unpaired electrons. This is due to alignment of magnetic moments in parallel and antiparallel directions in unequal number. | Fe3O4, MgFe2O4, ZnFe2O4 |
| Curie temperature | The temperature above which a ferromagnetic substance becomes paramagnetic. |
Electrical property of metals
| Piezoelectricity | Electricity caused due to mechanical stress. PbZrO3, NH4H2PO4, quartz. |
| Pyroelectricity | Electricity caused due to heating |
| Ferroelecticity | In piezoelectricity crystals, the dipoles remain permanently aligned in a particular direction even in the absence of external field. BaTiO3, Rochelle salt, KH2PO4 |
| Anti-ferroelectricity | Crystals in which dipoles are aligned in such a way that net dipole moment is zero.PbZrO3. |
For Short Question and Answer (CLICK)
For MCQ Test (CLICK)
For Practice Set (CLICK)