Study of Gas Law

The behavior of gases is fundamental to understanding a wide range of natural phenomena and technological applications. From the inflation of a balloon to the operation of internal combustion engines, gases play a crucial role. This chapter, “Study of Gas Laws,” delves into the relationships between the macroscopic properties of gases: pressure, volume, and temperature. We will explore the empirical laws discovered by pioneering scientists like Robert Boyle and Jacques Charles, which describe how these properties are interconnected under specific conditions. By understanding these gas laws, we gain valuable insights into the nature of gases and their predictable behavior, laying the groundwork for further exploration into thermodynamics and related fields. We will examine the simple mathematical relationships that govern these laws, and apply them to solve problems and understand real-world applications

Characteristics of Gases Based on Kinetic Theory

The kinetic theory of gases, also known as the kinetic molecular theory, provides a framework for understanding the behavior of gases. This theory is based on several postulates that describe the characteristics of gases at the molecular level.

Postulates of Kinetic Theory

1. Gases are composed of tiny particles called molecules: These molecules are in constant random motion.
2. The volume of gas molecules is negligible: The molecules are point particles with no volume.
3. Gas molecules are in constant motion: They move rapidly and randomly, colliding with each other and the walls of their container.
4. Collisions between gas molecules and the container walls are perfectly elastic: The molecules bounce off the walls without losing energy.
5. The average kinetic energy of gas molecules is directly proportional to the temperature: As temperature increases, the molecules move faster and have more kinetic energy.

Characteristics of Gases Based on Kinetic Theory

1. Pressure: The pressure of a gas is due to the collisions between gas molecules and the container walls. The more frequent and energetic the collisions, the higher the pressure.
2. Temperature: The temperature of a gas is a measure of the average kinetic energy of its molecules. Higher temperature means faster-moving molecules.
3. Volume: The volume of a gas is determined by the space between its molecules. As the molecules move faster and spread out, the volume increases.
4. Diffusion: Gases diffuse because their molecules are in constant random motion, allowing them to spread out and mix with other gases.
5. Expansion: Gases expand when heated because the increased kinetic energy of their molecules causes them to move faster and spread out.
6. Compressibility: Gases are compressible because their molecules can be forced closer together by increasing the pressure.

Numericals based on Boyle’s Law

1. A gas occupies 10.0 L at a pressure of 2.0 atm. What volume will it occupy if the pressure is increased to 4.0 atm, assuming the temperature remains constant?
2. A container of gas has a volume of 5.0 L at a pressure of 200 kPa. If the pressure is decreased to 100 kPa while keeping the temperature constant, what is the new volume?
3. A gas has an initial volume of 250 mL at a pressure of 760 mmHg. If the pressure is increased to 1520 mmHg, what is the final volume, assuming constant temperature?
4. If a gas occupies 3.0 m³ at a pressure of 1.0 atm, what pressure is required to compress the gas to a volume of 1.5 m³, assuming constant temperature?
5. A balloon contains 8.0 L of air at a pressure of 101.3 kPa. If the pressure is increased to 202.6 kPa, what is the new volume of the balloon?
6. A gas has a volume of 12.0 L at a pressure of 0.5 atm. What will the volume be if the pressure is increased to 1.5 atm, with the temperature held constant?
7. A gas sample has a volume of 500 mL at a pressure of 800 torr. What volume will it occupy at a pressure of 400 torr, if the temperature remains constant?
8. A gas occupies 2.5 L at 300 kPa. What pressure is required to compress it to 1.0 L at constant temperature?
9. A container holds 15 L of nitrogen gas at 1.2 atm. The gas is compressed to a volume of 5L. What is the new pressure?
10. A gas inside of a piston chamber has a volume of 600ml at a pressure of 2 atm. If the piston is pushed inward, and the new volume is 200ml, what is the new pressure inside of the chamber?
11. A gas has an initial volume of 5 L at a pressure of 3 atm. If the pressure is increased to 6 atm at constant temperature, what will be the final volume?
12. A balloon has a volume of 10 L at a pressure of 2 atm. What will be its volume if the pressure is reduced to 0.5 atm, assuming temperature remains constant?
13. A sample of gas at 1 atm occupies a volume of 8 L. What will be its pressure if the volume is decreased to 4 L while keeping the temperature constant?
14. A gas is initially at a pressure of 750 mmHg and occupies 12 L. If the volume decreases to 8 L, what will be the new pressure of the gas?
15. A container holds a gas at a volume of 20 L and a pressure of 5 atm. If the gas is compressed to 10 L, what is the new pressure?
16. A scuba diver’s tank contains air at 200 atm in a volume of 3 L. If the air is released to a volume of 30 L, what will be the pressure?
17. A gas at 4 atm pressure occupies 15 L. If the pressure is changed to 10 atm, what will be the new volume?
18. A cylinder of gas is at 1.2 atm and occupies 25 L. If the volume is expanded to 50 L, what will be the final pressure?
19. A gas sample is confined in a 6 L container at a pressure of 3 atm. If the pressure is decreased to 1 atm, what will be the final volume?
20. A syringe contains 40 mL of air at a pressure of 1 atm. If the plunger is pushed to reduce the volume to 10 mL, what will be the pressure inside the syringe?
21. A gas occupies a volume of 500 mL at a pressure of 2 atm. What will be its volume at a pressure of 1 atm?
22. A cylinder contains 20 L of oxygen at a pressure of 3 atm. If the pressure is increased to 4 atm, what will be the new volume of oxygen?
23. A gas has an initial volume of 200 mL and an initial pressure of 1.5 atm. If the pressure is increased to 2.5 atm, what will be the new volume?
24. A scuba tank contains 50 L of air at a pressure of 10 atm. If the pressure is decreased to 5 atm, what will be the new volume of air?
25. A gas occupies a volume of 1.5 L at a pressure of 2.2 atm. What will be its volume at a pressure of 1.1 atm?
26. A cylinder contains 30 L of helium at a pressure of 2.5 atm. If the pressure is increased to 3.5 atm, what will be the new volume of helium?
27. A gas has an initial volume of 400 mL and an initial pressure of 1.2 atm. If the pressure is decreased to 0.8 atm, what will be the new volume?
28. A balloon contains 2 L of air at a pressure of 1.1 atm. If the pressure is increased to 1.5 atm, what will be the new volume of air?
29. A gas occupies a volume of 800 mL at a pressure of 1.8 atm. What will be its volume at a pressure of 0.9 atm?
30. A cylinder contains 40 L of nitrogen at a pressure of 2.8 atm. If the pressure is decreased to 1.4 atm, what will be the new volume of nitrogen?

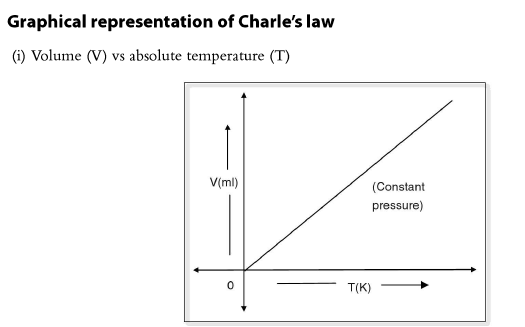
Numerical Problems based on Charles’ Law

1. A gas occupies a volume of 500 mL at a temperature of 27°C. What will be its volume at a temperature of 77°C?
2. A balloon contains 2 L of air at a temperature of 17°C. If the temperature is increased to 37°C, what will be the new volume of air?
3. A gas has an initial volume of 200 mL and an initial temperature of 20°C. If the temperature is increased to 80°C, what will be the new volume?
4. A cylinder contains 30 L of oxygen at a temperature of 10°C. If the temperature is decreased to -10°C, what will be the new volume of oxygen?
5. A gas occupies a volume of 1.5 L at a temperature of 25°C. What will be its volume at a temperature of 125°C?
6. A balloon contains 3 L of air at a temperature of 30°C. If the temperature is increased to 60°C, what will be the new volume of air?
7. A gas has an initial volume of 400 mL and an initial temperature of 15°C. If the temperature is decreased to -15°C, what will be the new volume?
8. A cylinder contains 40 L of nitrogen at a temperature of 20°C. If the temperature is increased to 80°C, what will be the new volume of nitrogen?
9. A gas occupies a volume of 2 L at a temperature of 35°C. What will be its volume at a temperature of 95°C?
10. A balloon contains 1.8 L of air at a temperature of 22°C. If the temperature is decreased to 2°C, what will be the new volume of air?
11. A gas has a volume of 500 mL at 27°C. What will be its volume at 127°C if pressure remains constant?
12. A balloon with a volume of 2.5 L is kept at 300 K. If the temperature is increased to 450 K, what will be the new volume?
13. A gas occupies 600 cm³ at 20°C. Find its volume at 100°C, assuming constant pressure.
14. A gas sample has an initial volume of 1.2 L at 250 K. What will be its volume at 400 K, assuming pressure is constant?
15. A 3 L gas is cooled from 500 K to 250 K. What is its final volume?
16. A gas at 0°C occupies 4.5 L. What will be its volume at 50°C if pressure remains unchanged?
17. A gas cylinder contains 10 L of gas at 350 K. If the temperature drops to 175 K, what will be the final volume?
18. A balloon has a volume of 1.8 L at 27°C. If it is heated to 327°C, what will be the new volume?
19. A gas occupies 750 mL at 400 K. Find its volume when cooled to 200 K under constant pressure.
20. A gas sample is kept at 20°C with a volume of 5 L. If the temperature increases to 100°C, what will be the final volume?
21. A gas occupies a volume of 5.0 L at 27°C. What volume will it occupy at 227°C, assuming constant pressure?
22. A balloon contains 10 L of air at 300 K. If the temperature is increased to 600 K, what will be the new volume of the balloon, assuming constant pressure?
23. A gas has a volume of 250 mL at 0°C. What will its volume be at 100°C, with constant pressure?
24. If a gas occupies 2.0 m³ at 150 K, what temperature (in Kelvin) is required to increase the volume to 4.0 m³, assuming constant pressure?
25. A container of gas has a volume of 8.0 L at 25°C. What will the volume be if the temperature is decreased to -25°C, assuming constant pressure?
26. A gas sample has a volume of 12.0 L at 300K. What is the volume of the gas if the temperature is changed to 450K, while the pressure is held constant?
27. A balloon has a volume of 5.0 L at 298 K. What temperature in Kelvin is needed to increase the volume to 7.5L, while pressure remains constant?
28. A gas occupies 100mL at standard temperature. What is the gasses volume at 546K, with constant pressure?
29. A gas inside a cylinder has a volume of 3L at 30 degrees celsius. What is the new volume of the gas if the temperature is changed to 60 degrees celsius, with constant pressure?
30. A gas sample is at a volume of 7.0L at a temperature of 200K. If the volume is decreased to 3.5L, what is the new temperature in Kelvin?

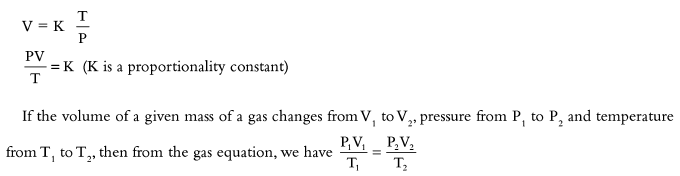
Numerical Problems on the Combined Gas Equation

1. A gas occupies a volume of 500 mL at a pressure of 2 atm and a temperature of 27°C. If the pressure is increased to 3 atm and the temperature is increased to 77°C, what will be the new volume of the gas?
2. A cylinder contains 20 L of oxygen at a pressure of 3 atm and a temperature of 17°C. If the pressure is decreased to 2 atm and the temperature is increased to 37°C, what will be the new volume of oxygen?
3. A gas has an initial volume of 200 mL, an initial pressure of 1.5 atm, and an initial temperature of 20°C. If the pressure is increased to 2.5 atm and the temperature is increased to 80°C, what will be the new volume?
4. A scuba tank contains 50 L of air at a pressure of 10 atm and a temperature of 10°C. If the pressure is decreased to 5 atm and the temperature is increased to 30°C, what will be the new volume of air?
5. A gas occupies a volume of 1.5 L at a pressure of 2.2 atm and a temperature of 25°C. If the pressure is increased to 3.2 atm and the temperature is decreased to -15°C, what will be the new volume?
6. A cylinder contains 30 L of helium at a pressure of 2.5 atm and a temperature of 30°C. If the pressure is decreased to 1.5 atm and the temperature is increased to 60°C, what will be the new volume of helium?
7. A gas has an initial volume of 400 mL, an initial pressure of 1.2 atm, and an initial temperature of 15°C. If the pressure is increased to 2.2 atm and the temperature is decreased to -20°C, what will be the new volume?
8. A balloon contains 2 L of air at a pressure of 1.1 atm and a temperature of 20°C. If the pressure is increased to 1.5 atm and the temperature is increased to 40°C, what will be the new volume of air?
9. A gas occupies a volume of 800 mL at a pressure of 1.8 atm and a temperature of 35°C. If the pressure is decreased to 0.8 atm and the temperature is decreased to -10°C, what will be the new volume?
10. A cylinder contains 40 L of nitrogen at a pressure of 2.8 atm and a temperature of 20°C. If the pressure is increased to 3.8 atm and the temperature is increased to 80°C, what will be the new volume of nitrogen?
11. A gas has an initial volume of 5 L at a pressure of 2 atm and a temperature of 300 K. What will be its volume if the pressure changes to 4 atm and the temperature to 600 K?
12. A gas sample is at 1.5 atm, 2.5 L, and 350 K. If its pressure is increased to 3 atm and the temperature to 700 K, find the new volume.
13. A balloon containing 3 L of gas at 27°C and 1 atm is taken to a place where the pressure is 0.5 atm and the temperature is 127°C. What will be its final volume?
14. A gas occupies 600 mL at 2 atm and 400 K. If its volume is increased to 1200 mL and the temperature is raised to 800 K, find the new pressure.
15. A gas is stored at 3 atm pressure, 5 L volume, and 273 K temperature. If the pressure is changed to 1 atm and the volume to 10 L, what will be the new temperature?
16. A 2 L gas sample at 250 K and 4 atm expands to 5 L. If the final pressure is 2 atm, what is the final temperature?
17. A gas at 1 atm and 273 K occupies a volume of 10 L. If the gas is compressed to 5 L and the temperature increases to 546 K, what will be the final pressure?
18. A gas sample has an initial state of 1 atm, 4 L, and 300 K. It undergoes a change where the new conditions are 2 atm and 600 K. What is the final volume?
19. A gas cylinder has a volume of 20 L at 400 K and 5 atm pressure. What will be the pressure if the volume is reduced to 10 L and the temperature drops to 200 K?
20. A gas is at 10 L, 3 atm, and 500 K. If its volume increases to 20 L and the pressure changes to 1.5 atm, what will be the final temperature?
21. A gas occupies 10.0 L at 2.0 atm and 27°C. What volume will it occupy at 1.0 atm and 227°C?
22. A container of gas has a volume of 5.0 L at 200 kPa and 300 K. If the pressure is decreased to 100 kPa and the temperature is increased to 450 K, what is the new volume?
23. A gas has an initial volume of 250 mL at 760 mmHg and 0°C. If the pressure is increased to 1520 mmHg and the temperature is increased to 100°C, what is the final volume?
24. If a gas occupies 3.0 m³ at 1.0 atm and 150 K, what pressure is required to compress the gas to a volume of 1.5 m³ at 300 K?
25. A balloon contains 8.0 L of air at 101.3 kPa and 25°C. If the pressure is increased to 202.6 kPa and the temperature is decreased to -25°C, what is the new volume of the balloon?
26. A gas has a volume of 12.0 L at 0.5 atm and 300 K. What will the volume be if the pressure is increased to 1.5 atm and the temperature is increased to 450 K?
27. A gas sample has a volume of 500 mL at 800 torr and 20°C. What volume will it occupy at 400 torr and 40°C?
28. A gas occupies 2.5 L at 300 kPa and 300 K. What pressure is required to compress it to 1.0 L at 600 K?
29. A container holds 15 L of nitrogen gas at 1.2 atm and 280 K. The gas is compressed to a volume of 5 L, and the temperature is increased to 350 K. What is the new pressure?
30. A gas inside of a piston chamber has a volume of 600ml at a pressure of 2 atm and a temperature of 27 degrees celsius. If the piston is pushed inward, and the new volume is 200ml, and the temperature is raised to 200 degrees celsius, what is the new pressure inside of the chamber?

Applications of Boyle’s Law

Boyle’s Law has numerous practical applications in various fields, including:

Medical Applications

1. Ventilators: Boyle’s Law is used to calculate the pressure and volume of air delivered to patients through ventilators.
2. Anesthesia: Anesthesiologists use Boyle’s Law to calculate the pressure and volume of anesthetic gases.
3. Respiratory Therapy: Respiratory therapists use Boyle’s Law to calculate the pressure and volume of oxygen delivered to patients.

Industrial Applications

1. Compressors: Boyle’s Law is used to design and operate compressors, which compress gases to high pressures.
2. Pneumatic Systems: Pneumatic systems, such as those used in factories and manufacturing plants, rely on Boyle’s Law to operate.
3. Scuba Tanks: Scuba tanks are designed using Boyle’s Law to store compressed air for underwater diving.

Scientific Applications

1. Gas Chromatography: Gas chromatography, a technique used to separate and analyze gases, relies on Boyle’s Law.
2. Mass Spectrometry: Mass spectrometry, a technique used to analyze the mass-to-charge ratio of ions, uses Boyle’s Law to calculate gas pressures.
3. Aerospace Engineering: Aerospace engineers use Boyle’s Law to design and operate spacecraft and aircraft systems.

Everyday Applications

1. Bicycle Tires: Boyle’s Law is used to calculate the pressure and volume of air in bicycle tires.
2. Air Conditioning: Air conditioning systems use Boyle’s Law to calculate the pressure and volume of refrigerant gases.
3. Diving: Scuba divers use Boyle’s Law to calculate the pressure and volume of air in their tanks.

Other Applications

1. Weather Forecasting: Meteorologists use Boyle’s Law to calculate the pressure and volume of air in weather systems.
2. Oil and Gas Industry: The oil and gas industry uses Boyle’s Law to calculate the pressure and volume of fluids in pipelines and storage tanks.
3. Cryogenics: Cryogenic systems, which operate at very low temperatures, use Boyle’s Law to calculate the pressure and volume of gases.

Applications of Charles’ Law

Charles’ Law has numerous practical applications in various fields, including:

Aerospace and Aviation

1. Airplane Tires: Charles’ Law is used to calculate the pressure and volume of air in airplane tires as temperature changes.
2. Hot Air Balloons: Hot air balloons rely on Charles’ Law to lift off the ground and float in the air.
3. Rocket Propulsion: Charles’ Law is used to calculate the pressure and volume of gases in rocket propulsion systems.

Industrial Applications

1. Refrigeration Systems: Refrigeration systems, such as those used in air conditioning and refrigeration, rely on Charles’ Law to operate.
2. Compressed Air Systems: Compressed air systems, used in various industrial applications, rely on Charles’ Law to calculate the pressure and volume of air.
3. Gas Cylinders: Gas cylinders, used to store gases such as oxygen and nitrogen, rely on Charles’ Law to calculate the pressure and volume of the gas.

Medical Applications

1. Anesthesia Machines: Anesthesia machines use Charles’ Law to calculate the pressure and volume of anesthetic gases.
2. Ventilators: Ventilators use Charles’ Law to calculate the pressure and volume of air delivered to patients.
3. Oxygen Tanks: Oxygen tanks, used to store oxygen for medical purposes, rely on Charles’ Law to calculate the pressure and volume of oxygen.

Scientific Applications

1. Thermometry: Thermometry, the science of measuring temperature, relies on Charles’ Law to calculate the pressure and volume of gases.
2. Gas Chromatography: Gas chromatography, a technique used to separate and analyze gases, relies on Charles’ Law.
3. Mass Spectrometry: Mass spectrometry, a technique used to analyze the mass-to-charge ratio of ions, uses Charles’ Law.

Everyday Applications

1. Bicycle Tires: Charles’ Law is used to calculate the pressure and volume of air in bicycle tires as temperature changes.
2. Car Tires: Car tires rely on Charles’ Law to calculate the pressure and volume of air as temperature changes.
3. Scuba Diving: Scuba divers use Charles’ Law to calculate the pressure and volume of air in their tanks as temperature changes.

Try Out # 1

1. According to Boyle’s Law, the volume of a gas is ___________ proportional to the pressure.
2. The Combined Gas Equation is given by P1V1/T1 = ___________.
3. Charles’ Law states that the volume of a gas is directly proportional to the ___________.
4. According to Boyle’s Law, P1V1 = ___________.
5. The Combined Gas Equation is a combination of Boyle’s Law, Charles’ Law, and the ___________ Law.
6. According to Boyle’s law, at constant temperature, the product of pressure and volume is __.
7. Charles’ law states that at constant pressure, the volume of a gas is __ proportional to its absolute temperature.
8. In the combined gas equation, the temperature must always be expressed in __.
9. If the volume of a gas is doubled while keeping the temperature constant, its pressure will become __.
10. According to Boyle’s Law, at constant temperature, the volume of a gas is inversely proportional to its __.
11. Charles’s Law states that at constant pressure, the volume of a gas is directly proportional to its __ temperature.
12. The combined gas law combines Boyle’s Law and Charles’s Law, and is expressed as __.
13. When using gas laws, temperature must always be in __.
14. If pressure is held constant and temperature increases, the volume of a gas will __.
    
15. Which law states that the volume of a gas is directly proportional to the temperature?
    a) Boyle’s Law
    b) Charles’ Law
    c) Gay-Lussac’s Law
    d) Avogadro’s Law
16. What is the relationship between pressure and volume according to Boyle’s Law?
    a) Directly proportional
    b) Inversely proportional
    c) Constant
    d) None of the above
17. Which equation represents the Combined Gas Equation?
    a) P1V1 = P2V2
    b) V1/T1 = V2/T2
    c) P1V1/T1 = P2V2/T2
    d) P1/P2 = V2/V1
18. According to Charles’ Law, what happens to the volume of a gas when the temperature is increased?
    a) Decreases
    b) Increases
    c) Remains constant
    d) Becomes zero
19. Which law is not included in the Combined Gas Equation?
    a) Boyle’s Law
    b) Charles’ Law
    c) Gay-Lussac’s Law
    d) Avogadro’s Law
20. Boyle’s law states that the relationship between pressure and volume of a gas is:
    a) Directly proportional
    b) Inversely proportional
    c) Exponentially related
    d) Unrelated
21. What happens to the volume of a gas if its temperature is increased from 300 K to 600 K while pressure remains constant?
    a) It doubles
    b) It remains the same
    c) It decreases
    d) It becomes half
22. In the combined gas equation, if the temperature is kept constant, it reduces to:
    a) Boyle’s law
    b) Charles’ law
    c) Ideal gas law
    d) Dalton’s law
23. A balloon shrinks when placed in a refrigerator because:
    a) The pressure inside increases
    b) The temperature decreases, reducing volume
    c) The gas molecules escape
    d) The number of moles decreases
24. If the pressure and temperature of a gas both double, what happens to its volume?
    a) It doubles
    b) It remains the same
    c) It becomes half
    d) It quadruples
25. Which law describes the relationship between pressure and volume at constant temperature?
    a) Charles’s Law
    b) Boyle’s Law
    c) Combined Gas Law
    d) Ideal Gas Law
26. If the temperature of a gas is doubled and the pressure is kept constant, what happens to the volume?
    a) It halves
    b) It doubles
    c) It remains the same
    d) It quadruples
27. The combined gas law formula is:
    a) PV = nRT
    b) P₁V₁ = P₂V₂
    c) V₁/T₁ = V₂/T₂
    d) (P₁V₁) / T₁ = (P₂V₂) / T₂
28. What unit must temperature be in when using the gas laws?
    a) Celsius
    b) Fahrenheit
    c) Kelvin
    d) Any unit is fine
29. If a gas is compressed at constant temperature, what happens to its pressure?
    a) It decreases
    b) It increases
    c) It remains the same
    d) It fluctuates

Try Out #2

1. What is the relationship between pressure and volume according to Boyle’s Law?
2. Which law states that the volume of a gas is directly proportional to the temperature?
3. What is the Combined Gas Equation?
4. State Boyle’s Law and explain its significance.
5. Describe the relationship between pressure and volume according to Charles’ Law.
6. Explain the significance of Boyle’s Law in real-life applications.
7. Describe the relationship between pressure, volume, and temperature of a gas.
8. Plot a graph showing the relationship between pressure and volume according to Boyle’s Law.
9. Plot a graph showing the relationship between temperature and volume according to Charles’ Law.
10. A gas is compressed from a volume of 500 mL to 200 mL. What will be the new pressure if the initial pressure was 2 atm? (Use Boyle’s Law)
11. A cylinder contains 20 L of oxygen at a temperature of 17°C. If the temperature is increased to 37°C and the pressure is decreased to 1 atm, what will be the new volume of oxygen? (Use the Combined Gas Equation)
12. A gas has an initial volume of 200 mL, an initial pressure of 1.5 atm, and an initial temperature of 20°C. If the pressure is increased to 2.5 atm, the temperature is increased to 80°C, and the volume is decreased to 100 mL, what will be the new pressure? (Use the Combined Gas Equation)
13. What happens to the volume of a gas if the pressure is doubled while keeping temperature constant?
14. A gas at 2 atm has a volume of 6 L. If the pressure increases to 4 atm, find the new volume.
15. How does Boyle’s law explain the working of a syringe?
16. Draw and explain the pressure vs. volume graph for Boyle’s law.
17. A scuba diver breathes air at 4 atm in deep water. What will happen to the air volume if he ascends to a region with 2 atm pressure?
18. Convert the pressure from mmHg to atm before solving a Boyle’s law problem.
19. Why do hot air balloons rise according to Charles’ law?
20. A gas has a volume of 3 L at 300 K. What will be its volume at 450 K, assuming constant pressure?
21. How does Charles’ law apply to a car tire in winter and summer?
22. Sketch and explain the volume vs. temperature graph for Charles’ law.
23. A balloon at room temperature (20°C) has a volume of 2 L. What will be its volume at 100°C?
24. Convert the temperature from Celsius to Kelvin before solving a Charles’ law problem.
25. How does the combined gas law integrate Boyle’s and Charles’ laws?
26. A gas at 2 atm, 5 L, and 300 K is changed to 4 atm and 600 K. Find the new volume.
27. How does the combined gas law help in predicting the behavior of gases in weather balloons?
28. What happens to a gas sample if its temperature is doubled, volume is halved, and pressure remains constant?